最近在看Hierarchical Dirichlect Process(Yee Whye TEH,Michael I. JORDAN)這篇論文,第一次接觸這樣的主題,整理了一下我自己的心得~~~
為什麼要用Hierarchical Dirichlet Process?
舉例來說,在信息檢索領域中,常常我們需要去將不同的文章去分主題,比如說今天有一篇文章”林書豪和周杰倫出新歌”,那這篇文章可能的主題是”運動”和”音樂”,這時候我們可以用DPMM去將這一個文章分成這些主題,但如果今天又有另一篇文章”王建民回國擔任投手,為國爭光”,這篇文章可能的主題是”運動”和”國家”,那又只能用另一個DPMM模型去分類,此時出現一個問題,這兩篇都有一個共同主題”運動”,但是不同的DPMM模型分類為運動,可能用不同的標籤做代表,就會出現同一標籤出現不同主題的情況,無法做到資訊共享,不然就需要將這兩篇文章合併成一篇文章,再使用DPMM去做分類。
那我會先從DP開始,然後再說明HDP
一.DP介紹:
DP是一個隨機過程,是由很多個Dirichlet分布所組成,首先先簡單描述一下Dirichlet分布是什麼?
假設今天我們擲一個正反兩面的不公平硬幣(Bernouli分布),要如何算擲硬幣後正面的機率為多少?
我們會先假設先驗機率來自Beta分布,然後透過擲硬幣後得到的資料推算出後驗機率,因為共軛性(Conjugate),後驗機率也會是Beta分布,當今天擲很多種不同硬幣時就會變成Bernouli Process。
同樣的情況推廣至多維時,變成擲一個骰子(Mutinomial分布),此時我們的先驗機率會變成Dirchlet分布,一次模擬骰子每個面的機率,也就是Beta分布的推廣,同樣的先驗機率和後驗機率也具有共軛性(Conjugate),後驗機率也會是Dirchlet分布,同樣當今天擲很多種不同骰子時就變成Dirichlet Process。
因此在分類文章主題上,不同主題(骰子)由不同字(骰子的不同面)所組成,為Mutinomial分布,多個主題組成一個文章形成混合分布,我們希望從文章中分類出有什麼樣的主題,這時就需要Dirichlet Process去抽出很多的參數,來看哪些屬於同分布(同參數)。
那為什麼需要使用Dirichlet Process作為我們的先驗分布呢?
因為我們的數據是來自一個混合分布,即n個數據來自k個分布,其中n >= k,因此對於同一分布的觀測值,其分布的參數會是一樣的,但如果先驗是連續分布,那麼抽樣結果不可能出現相同的值,可以由下面的數學公式得知,\(\theta_{1}\)和\(\theta_{2}\)是由連續分布所產生,透過變數變換的方式讓 \(Y = \theta_{1}-\theta_{2}\), 因為連續分布單點並不存在機率,因此可得知\(\theta_{1}\)等於\(\theta_{2}\)的機率為零
\[P(\theta_{1}=\theta_{2})=P(\theta_{1}-\theta_{2}=0)=P(Y=0)=0\]因此我們可以透過DP的特性,來解決這樣的問題,DP有兩個參數\(\alpha\)和\(H\),\(H\)是一個連續分布,而我們的參數並不希望從連續分布裡抽出來,需要有一點離散,這樣才會抽到不同的值,達到分群的效果,因此我們會透過\(\alpha\)這個參數去控制離散的程度,當\(\alpha\)很大時,G會很不離散,當\(\alpha\)很小時,G會變得很離散。
以數學表示如下:
\(\theta_i\)來自G分布,G分布則是從DP裡抽出來,每次從DP抽都會是一個分布,所以有人會說DP是分布的分布。
\[\theta_i \sim G\] \[G \sim DP(\alpha,H)\]下圖紅色的長條就是我們從DP抽出來的G分布,可以看到是離散的,藍色是H分布,除此之外還可以看到黃色的長條將G分布分成三等份,這是DP的另外一個特性,DP抽出來的G分布對其任意劃分會是Dirichlet分布,也就是說G分布的邊際分布會是Dirichlet分布,用數學表示如下:
\[(G(a_1),G(a_2),....,G(a_k)) \sim DIR(\alpha H(a_1),\alpha H(a_2),.....,\alpha H(a_k)) <=> G \sim DP(\alpha,H),\text{for all partition}\,\alpha_1,\alpha_2,....,\alpha_k\]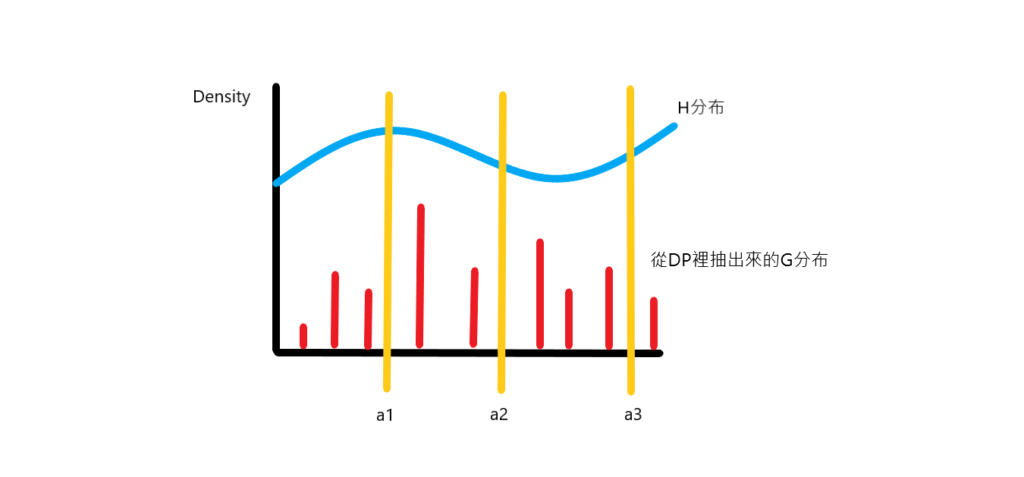
二.DP的性質
DP的性質主要可以由三種不同的觀點去說明:
1.The Stick-Breaking Construction:
這種方法可以說明從DP抽出來的分布有離散性且機率加總為一,那是如何做的呢?
假設我們今天有一根棍子,棍子的長度為1公分,一開始我們從\(Beta(1,\alpha)\)中先抽出一個數字(\(\alpha\)是之前提到用來控制DP離散程度的參數),假設抽到0.2,那我們就將棍子長度0.2的部分折斷當作我們第一個權重\(\pi_1\),也就是\(1 \times 0.2=0.2\)公分,然後再從\(Beta(1,\alpha)\)中抽出一個數字,假設抽到0.3,那我們就是從剩下的棍子長度為0.8中拿走0.3的部分,當作我們的第二個權重,也就是\(0.8 \times 0.3=0.24\)公分,然後如此下去,直到棍子被折完為止。
示意圖如下:
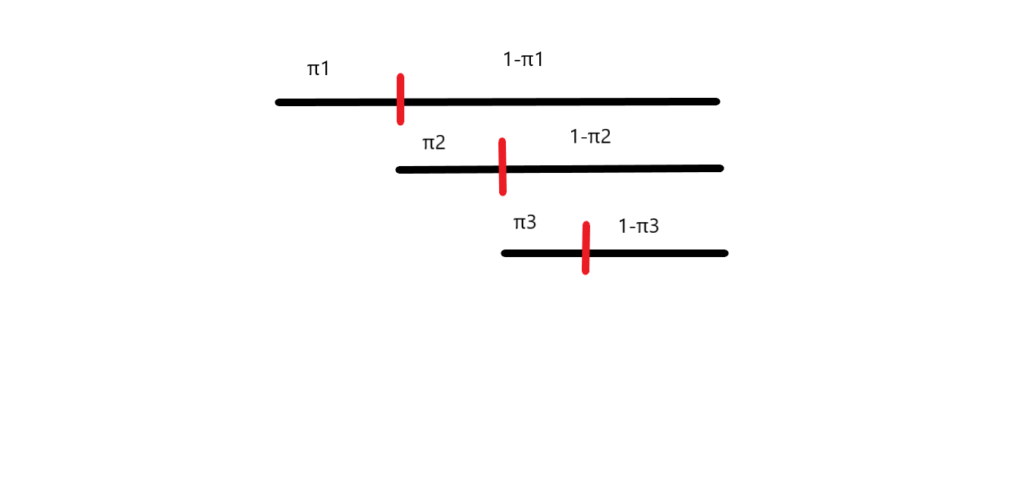
以數學形式表示如下,\(\pi_k^{‘}\)就是我們每次抽出來的值,透過乘以扣掉前面權重的值得到當前權重,而\(\phi_k\)則是該權重在機率分布上的值:
\[\pi_k^{'}|\alpha,H\,\sim beta(1,\alpha)\,,\,\pi_k=\pi_k^{'}\prod_{l=1}^{k-1}(1-\pi_l^{'}),\,\phi_k|\alpha,H\,\sim H\]因此如果我們以下面的方式定義隨機測度G會服從\(DP(\alpha,H)\),而\(\delta_{\phi_k}\)中文比較難解釋,原文是說\(\delta_{\phi_k}\) is a probability measure concentrated at \(\phi_k\),意思是\(\phi_k\)是從連續分布\(H\)裡抽出來的是一個隨機變量,以機率的方式來衡量抽到\(\phi_k\)的機率。
\[G=\sum_{k=1}^{\infty}\pi_k\delta_{\phi_k}\sim DP(\alpha,H)\]那為什麼說Stick-Breaking Construction可以顯現出DP的離散性?因為我們的權重是由\(Beta(1,\alpha)\)所抽出,計算期望值可知,當\(\alpha=0\)時抽出來的分佈最離散(只有一點),當\(\alpha=\infty\)時抽出來的分布變連續,透過\(\alpha\)我們可以控制抽出分布的離散程度。
\[\begin{eqnarray}&&E(\pi_k^{'})=\frac{1}{1+\alpha}\\ &&\alpha=0,E(\pi_k^{'})=1\,\,\text{權重全部分配到$\pi_1$,此時最離散}\\ &&\alpha=\infty,E(\pi_k^{'})=0\,\,\text{變成連續分配}\end{eqnarray}\]而抽出來的這些權重也相加等於一\(\sum_{k=1}^{\infty}\pi_k=1\),為了方便我們把抽出來的權重寫成\(\pi=(\pi_k)_{k=1}^{\infty}\),這裡的\(\pi\)也是隨機測度,由Griffiths,Engen,and McCloskey所定義,因此可以寫成\(\pi \sim GEM(\alpha)\)
我們用程式來實作Stick-Breaking Construction
我們分別畫出了在\(\alpha=2\)和\(\alpha=100\)的時候,透過Stick-Breaking Construction建構DP資料的分布情況,可以看到當\(\alpha=2\)時,資料分布是離散的,當我們將\(\alpha\)增大為100時,資料分布就變得沒那麼離散,到無限大時,就會變連續的。
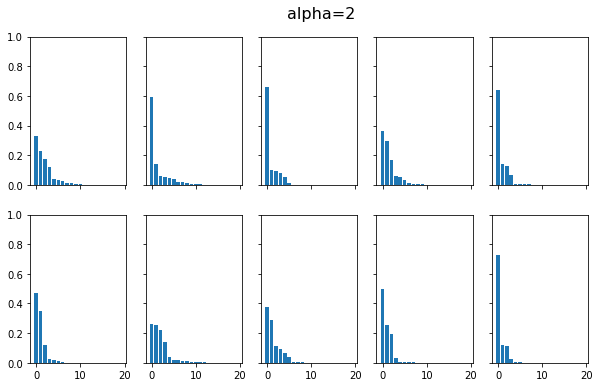
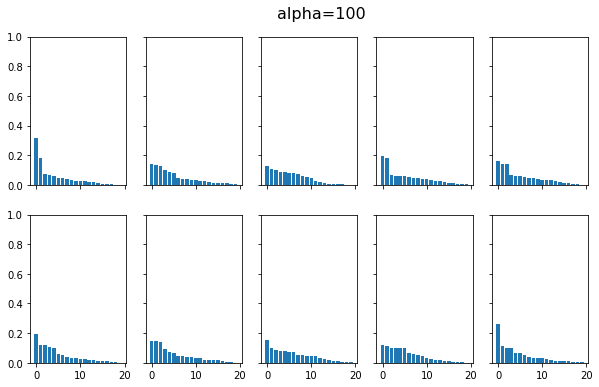
2.Chinese Restaurant Process(中國餐館過程):
透過中國餐館過程可以很好的說明DP的離散性和群聚的特性
中國餐館過程描述如下:
1.假設一個中國餐館中可以有無限的桌子
2.來吃飯的第一個顧客做第一張桌子
3.對於每一個顧客,都按照以下規則入座,\(n_k\)代表第k個桌子已有顧客數,\(n-1\)代表在這顧客之前,已有顧客總數
\[P(\theta_i|\theta_1,...,\theta_i,\alpha,H)=\left\{ \begin{aligned} &\frac{n_k}{n+\alpha-1}\quad,\text{顧客選擇坐在已有人桌子上的機率}\\ &\frac{\alpha}{n+\alpha-1}\quad,\text{顧客選擇坐在新的桌子上的機率} \end{aligned} \right.\]那就舉個例子來說明,看下面這張圖,假設這個餐館的桌子是無限的,紅色圈圈代表有人坐的桌子,綠色圈圈代表還沒有人坐的桌子,藍色圈圈代表顧客,
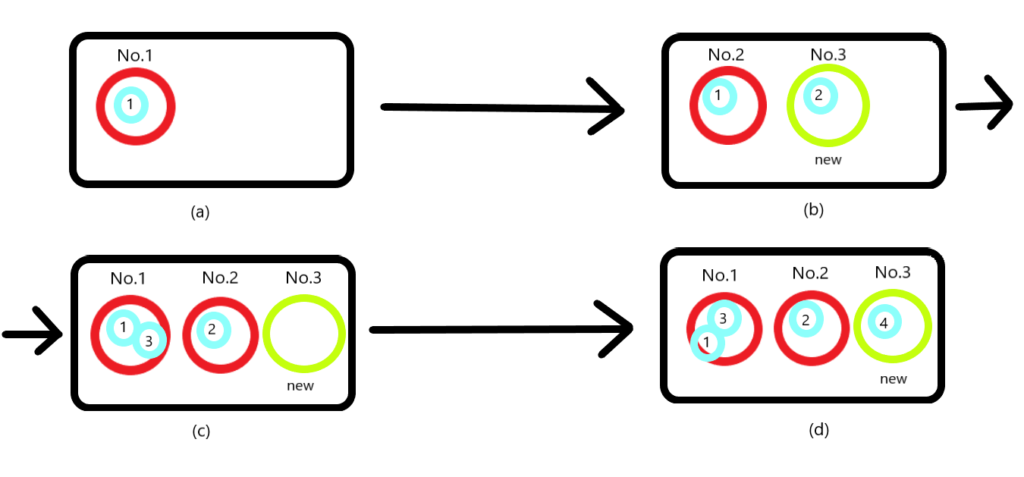
(a)第一個客人進入餐館,100%的機率會坐一張新桌子
(b)第二個客人進入餐館,第一張桌子已經坐了1號客人,所以第二個顧客坐第一張桌子的機率是\(\frac{1}{1+\alpha}\),坐新桌子的機率是\(\frac{\alpha}{1+\alpha}\),假設2號客人坐了第二張桌子
(c)第三個客人進入餐館,此時第三個客人坐第一張桌子的機率是\(\frac{1}{2+\alpha}\),坐第二張桌子的機率是\(\frac{1}{2+\alpha}\),坐新桌子的機率是\(\frac{\alpha}{2+\alpha}\),假設3號客人坐了第一張桌子
(d)第四個客人進入餐館,此時第一張桌子坐了兩人,所以四號客人坐第一張桌子的機率會增加,為\(\frac{2}{3+\alpha}\),坐2號桌的機率為\(\frac{1}{3+\alpha}\),坐新桌子的機率為\(\frac{\alpha}{3+\alpha}\)
從以上例子可以發現到,只要桌子越多人坐,新進來的顧客越可能去坐那張桌子,顯示出群聚的特性,另外參數\(\alpha\)值越大,新進來的客人坐新桌子的機率也會越大,這些桌子代表都是一篇文章的主題,而客人則是文章的文字。
3.Dirichlet Process Mixture Model:
在講第三種DP的觀點之前,我們先來介紹DP的應用-DPMM,DPMM就是一種混合模型可以用來分群,不同LDA的是,可以不用事先決定分群數量,透過以下數學式來說明其運作過程,首先我們的G是來自\(DP(\alpha,H)\),然後透過\(G\)產生很多個\(\theta\),從這些參數的分布產生\(x\),下圖則是視覺化模型生成數據的過程,紅色框框代表會不斷的重複此過程
\[G \sim DP(\alpha,H)\] \[\theta_1,\theta_2,....\theta_n \sim G\] \[x_i \sim F(\theta_i)\]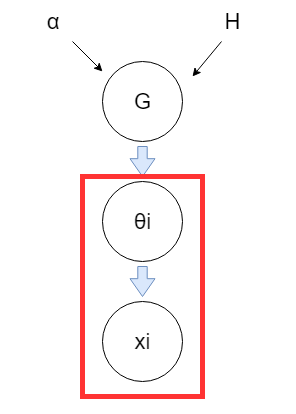
4.The Infinite Limit of Finite Mixture Models(有限混和模型的極限近似):
DPMM可以透過有限混合模型取極限後得到,之前我們在Stick-breaking Construction中定義\(G=\sum_{k=1}^{\infty}\pi_k\delta_{\phi_k}\),那在有限混合模型中我們假設有L個組成成分,因此我們可以定義\(G=\sum_{k=1}^{L}\pi_k\delta_{\phi_k}\),將其取極限即是DPMM。
那為什麼說DPMM可以不需要決定需要分群的數量?
因為我們使用DP作為我們的先驗分布,而我們數據來自一個混合分布,對於同一分布的觀察值,其分布的參數\(\theta\)會是一樣的。若我們使用連續分布作為先驗分布,那麼抽樣結果不可能出現相同的值,而DP的離散性可以解決這樣的問題,同時由於模型數據增長速度大於混合模型個數的增長,因此對一定樣本的數據,我們可以得到遠小於樣本類別的個數。
三.HDP介紹
那以上就是DP的介紹,DP只針對單一組數據或單一篇文章去分群,當有多組數據時,我們可以使用HDP將各組數據資訊共享,達到對多組數據分群的目的。
那要怎麼達到資訊共享呢?
假設對每組數據 j 都有一個與之相關的隨機測度\(G_j\),而\(G_j\)可以透過與該組相關的一個DP(\(G_j \sim DP(\alpha_{0j},G_{0j})\))得到,也就是每組數據都有一個DP,對於不同組的數據聚類,我們可以把不同小組的DP連結起來,意思是我們為不同小組數據做組內聚類,而組與組之間的類別可能是相同的,在文檔建模中,每個文章都是一組數據,都有多個主題生成,我們既要能對每個文章內的主題建模,同時保證不同文章間相同主題編號代表同一個主題,所以要將文章連接起來,有個很簡單的思路可以做到這些,就是將不同小組的\(G_j\)當作來自同一個先驗的結果,他們都共享一個DP先驗,即\(G_j \sim DP(\alpha_0,G_0)\),但有個問題,當\(G_0\)是一個連續分布的時候,儘管我們能夠通過DP的方式得到\(G_0\)的抽樣結果,但是這些抽樣結果\(G_j\)都不具有相同的值,也就是說雖然組內數據可以透過DP先驗得到一系列的分群結果,但組與組之間的分群標籤卻是不同的,所以作者限制\(G_0\)必須是離散的,以數學式表達如下:
\[G|\gamma,H \sim DP(\gamma,H)\] \[G_j|\alpha,G \sim DP(\alpha,G)\] \[\theta_{ji}|G_j \sim G_j\] \[x_{ji}|\theta_{ji} \sim F(\theta_{ji})\]跟DPMM比只是多新增了一個\(G\)作為各組數據\(G_j\)的先驗,HDP也一樣有Stick-Breaking Construction和Chinese Restaurant Franchise(剛剛是只有一家餐館,現在變很多家)描述HDP的特性
1.Stick-Breaking Construction(HDP):
在DP的時候,我們透過Stick-Breaking Construction建構\(G\),現在我們不只要建構\(G\)還要透過\(G\)建構各組數據的\(G_j\)。
這裡改一下符號原先用\(\pi\)作為抽出的權重,換成用\(\beta\)代替方便表示,這也是我們在DP的時候抽出的權重:
\[\beta_k^{'} \sim Beta(1,\gamma)\,,\beta_k=\beta_k^{'}\prod_{l=1}^{k-1}(1-\beta_l^{'})\]透過一些複雜的證明,我們可以知道利用各組數據的先驗分布\(G\)抽出來的權重\(\beta\),可以建構出各組數據\(G_j\)的權重:
\[\pi_{jk}^{'} \sim Beta(\alpha\beta_k,\alpha(1-\sum_{l=1}^{k-1}\beta_l))\,,\pi_{jk}=\pi_{jk}^{'}\prod_{l=1}^{k-1}(1-\pi_{jl}^{'})\]2.Chinese Restaurant Franchise:
一樣透過中國餐館特許經營可以很好的說明HDP的群聚性和離散性
中國餐館特許經營的過程描述如下:
假設我們有個全球連鎖的中國餐館,它們都有著相同的菜單,每個餐館都有無限的桌子,每張桌子可以坐無限的人
(a).第一個顧客進來後選了一張桌子,並點了一道菜。
(b).第二個顧客進來後可以選第一張桌子坐,也可以選新的桌子坐(注意,每個桌子的後來者點的菜都和坐該桌子第一個顧客點的菜一樣,因此後來者都不用點菜),如果第二個顧客坐上新的桌子,就要重新點菜,點的菜可以和第一桌點的一樣,也可以不一樣。
(c).不同的桌子可以點到相同的菜,不同的餐館的不同桌子也可能點到相同的菜,一直這樣進行下去,直到所有用戶入座就結束了。
看下面這張圖,這裡每個餐館j都相當於一組數據,每個顧客都是一個數據點所屬的混和分布的參數\(\theta_{ji}\),每個桌子都有指示變量\(\psi_{jt}\),它對應一道菜\(\phi_k\),用來表示每個顧客點哪道菜,而這道菜就是文檔主題,它就是來自\(H\),大家共享的一個參數
一句話總結這樣的過程:顧客 i 走進餐館 j,坐在桌子 \(t_{ji}\) 邊,而餐館 j 中的桌子對應一道菜\(\psi_{jt}\)
四.HDP inference
介紹完HDP的性質後,我們要開始對HDP進行推論(inference),我們會使用Gibbs sampler,一種基於中國餐館特許經營的方法進行說明。
有人說為什麼要對後驗分配進行採樣,而不直接利用公式直接把後驗分配算出來呢?
舉例來說:今天我們有一組資料,想要去看說看過資料後會有什麼樣的變化,我們會透過下面的公式去計算
\[P(\theta|Data) = \frac{P(Data|\theta) * P(\theta)}{P(Data)}\]但我們為了求得後驗機率必須計算\(P(Data)\),它的參數空間很巨大,很難去計算\(P(D)\),於是就提出透過採樣去逼近真實的後驗分配,而我們今天會使用Gibbs sampler對後驗分配搭配中國餐館特許經營進行採樣
\[P(D) = \int_\theta P(D,\theta)d\theta\]首先對我們會用到的變數進行說明
\(x_{ji} \sim F(\theta_{ji}) - 觀察資料\)
\(t_{ji} - 第 j 個餐館的第 i 個table\)
\(n_{jtk} - 第 j 個餐館的第 t 個table點的菜為 k 的客人數量\)
\(m_{jk} - 第 j 個餐館,點的菜為 k 的桌子數\)
\(z_{ji}=k_{jt_{ji}} - 為第 j 個餐廳的第 i 個客人在第 t 個桌子所點的菜\)
\(k_{jt} - 第 j 個餐館的第 t 個桌子點的菜\)
\(K - 全部餐廳總共點了多少不同的菜\)
因為\(F(\theta)\)的機率密度函數為\(f(\bullet|\theta)\),而H的機率密度函數為\(h(\bullet)\),且F和H共軛,因此我們可以透過對\(\phi\)積分,也就是對我們的mixture component(文章主題)做積分,可以得到\(x_{ji}\)的機率密度函數如下:
\[f_k^{-x_{ji}}(x_{ji})=\frac{\int f(x_{ji}|\phi_k)\prod_{j^{'}i^{'}\neq ji,z_{j^{'}i^{'}}=k}f(x_{j^{'}i^{'}}|\phi_k)h(\phi_k)d\phi_k}{\int \prod_{j^{'}i^{'}\neq ji,z_{j^{'}i^{'}}=k}f(x_{j^{'}i^{'}}|\phi_k)h(\phi_k)d\phi_k}\quad(1)\]式(2)為當顧客坐新桌子的時候,觀測數據\(x_{ji}\)的條件分布,等號右邊第一項是新的餐桌點之前點過的菜的機率和,等號右邊第二項則是新的餐桌點一道新的菜的機率
\[P(x_{ji}|t^{-ji},t_{ji}=t^{new},k) = \sum_{k=1}^{K}\frac{m_{\bullet k}}{m_{\bullet\bullet}+\gamma}f_k^{-x_{ji}}(x_{ji}) \,+\,\frac{\gamma}{m_{\bullet\bullet}+\gamma}f_{k^{new}}^{-x_{ji}}(x_{ji})\quad (2)\\ 其中f_{k^{new}}^{-x_{ji}}(x_{ji})=\int f(x_{ji}|\phi)h(\phi)d\phi\]1.採樣t:
在中國餐館特許經營的模式下,我們會先為每一位顧客分配餐桌,然後再點菜,有以下的關係存在,分別是顧客坐到有人的桌子的機率和新的桌子的機率,可以從公式得知當桌子有人坐的時候,人數越多,新客人越可能坐到那個位置,而坐到新桌子的機率由\(\alpha\)和式(2)所控制
\[P(t_{jt}=t|t^{-ji},k)\propto\left\{ \begin{aligned} &n_{jt\bullet}^{-ji} * f_{k_{jt}}^{-x_{ji}}(x_{ji}) \quad\quad\quad\quad\quad \text{if t previously used}\\ &\alpha * P(x_{ji}|t^{-ji},t_{ji}=t^{new},k) \quad \text{if t=\\(t^{new}\\)}\quad \end{aligned}\quad(3) \right.\]2.採樣k:
接著我們要為每個餐廳的每張桌子點菜,此時要分析的對象是不同餐廳的不同桌子點的菜色(共用同一張菜單),由公式可以發現到,越多人點的菜,客人點新的菜也傾向點那一種,而點到新的菜的機率由\(\gamma\)和\(f_{k^{new}}^{-x_{ji}}(x_{ji})\)所控制
\[P(k_{jt}=k|t,k^{-jt})\propto\left\{ \begin{aligned} &m_{\bullet k}^{-jt}f_{k}^{-x_{jt}}(x_{jt})\quad \text{if k is previously used}\\ &\gamma f_{k^{new}}^{-x_{jt}}(x_{jt})\quad\quad \text{if k=\\(k^{new}\\)} \end{aligned} \right.\]那以上就是關於HDP的介紹,如果有什麼問題大家可以在下方留言,我會盡力回答大家!!!如果喜歡我的文章,可以幫我拍拍手哦~~~

